Answer:
Part 1) The measure of the remaining angle is

Part 2) Is a 10 sided polygon (decagon)
Part 3) Yes, is possible for a triangle to have angles measures of 1°, 2° and 177°
Explanation:
Part 1)
we know that
The sum of the measures of the interior angles of a polygon is equal to the formula

where
n is the number of sides of polygon
In this problem we have a hexagon
so
n=6 sides
Substitute
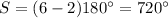
Let
x-----> the measure of remaining angle of the hexagon
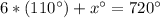
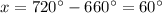
Part 2) The sum of the measures of the interior angles of a polygon is
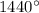 . What kind of polygon is it?
. What kind of polygon is it?
we know that
The sum of the measures of the interior angles of a polygon is equal to the formula

where
n is the number of sides of polygon
In this problem we have
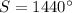
substitute in the formula and solve for n
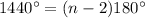
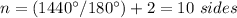
therefore
Is a 10 sided polygon (decagon)
Part 3) Is it possible for a triangle to have angles measures of 1°, 2° and 177° ?
we know that
In any triangle the sum of the measures of the interior angles must be equal to 180 degrees
In this problem we have
1°+ 2°+ 177°=180°
therefore
Yes, is possible for a triangle to have angles measures of 1°, 2° and 177°