Answer:
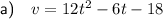

c) 1.5 s
d) -19.25 m
e) 24.5 m
Explanation:
Displacement

(where t ≥ 0 and x is in meters)
Part (a)
To find the equation for velocity, differentiate the equation for displacement:
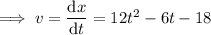
(where t ≥ 0 and v is in meters per second)
Part (b)
To find the equation for acceleration, differentiate the equation for velocity:
(where t ≥ 0 and a is in meters per second squared)
Part (c)
The particle comes to rest when its velocity is zero:
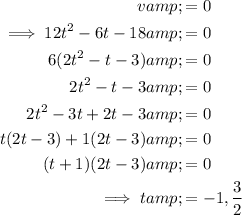
As t ≥ 0, the particle comes to rest at 1.5 s.
Part (d)
Substitute the found value of t from part (c) into the equation for displacement to find where the particle comes to rest:
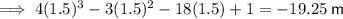
Part (e)
We have determined that the particle is at rest at 1.5 s.
Therefore, to find how far the particle traveled in the first 2 seconds, we need to divide the journey into two parts: before and after it was at rest.
The first leg of the journey is the first 1.5 s and the second leg of the journey is the next 0.5 s.
At the beginning of the journey, t = 0 s.
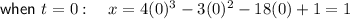
Therefore, when t = 0, x = 1
When t = 1.5 s, x = -19.25 m (from part (d)).
⇒ Total distance traveled in first 1.5 s = 1 + 19.25 = 20.25 m
When t = 2, x = -15 m.
Therefore, the particle has traveled 19.25 - 15 = 4.25 m in the last 0.5 s of its journey.
Total distance traveled:
1 + 19.25 + 4.25 = 24.5 m
Refer to the attached diagram
When the particle is at rest, it changes direction. If we model its journey using the x-axis, for the first leg of its journey (0 - 1.5 s) it travels in the negative direction (to the left). At 1.5 s it stops, then changes direction and travels in the positive direction (to the right), arriving at -15 at 2 seconds.