Answer:
2.3%
Explanation:
The formula to convert x into z distribution is

Where z is the test statistic
x is what we are looking for (in this case 37)
 is the mean (in this case, it is 25)
is the mean (in this case, it is 25)
 is the standard deviation (we have 6)
is the standard deviation (we have 6)
Plugging these into the formula, we get:
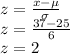
Thus we can say we want
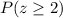
Note:
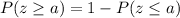
The table given is for any z where

Thus, now we have:
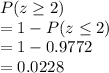
0.0228 into percentage is 0.0228 * 100 = 2.28%
Rounded, we get 2.3%
Third answer choice is right.