Question

The function f(x) is shown on the provided graph. Graph the result of the following transformation on f(x).

Answer 1

Observe the attached image

Explanation:

We have the graph of a line that passes through the points (0,5) and (2, 1).

The equation of the line that passes through these points is found in the following way:

`y = mx + b`

Where

m = slope

`m = \frac {y_2-y_1}{x_2-x_1}\\\\m = (1-5)/(2-0)\\\\m = -2\\\\b = y_2-mx_2\\\\b = 1 -(-2)(2)\\\\b = 5`

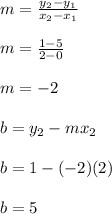
So

`y = -2x + 5`

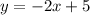
We must apply to this function the transformation
`f (x-4)`.

We know that a transformation of the form

`y = f (x + h)` shifts the graph of the function f(x) h units to the right if
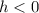`h <0`, or shifts the function f(x) h units towards the left if
`h> 0`.

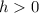In this case
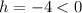`h = -4 <0` then the transformation
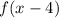`f(x-4)` displaces the graph 4 units to the right.

Therefore if f(x) passes through the points (0,5) and (2,1) then
`f (x-4)` passes through the points (4, 5) (6, 1)

And its equation is:

`y = -2(x-4) +5\\\\y = -2x +13`

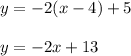
Observe the attached image