Question

At a local company, the ages of all new employees hired during the last 10 years are normally distributed. The mean age is 31 years old, with a standard deviation of 10 years. If you were to take a sampling of 10 employees, what is the probability your mean age will be at least 28? Round to the nearest percent.

Answer 1

P = 83%

Explanation:

In this problem we have the ages of all new employees hired during the last 10 years of normally distributed.

We know that the mean is
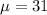`\mu = 31` years and standard deviation is
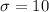`\sigma = 10` years

By definition we know that if we take a sample of size n of a population with normal distribution, then the sample will also have a normal distribution with a mean

`\mu_m = \mu`

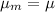
And with standard deviation

`\sigma_m = (\sigma)/(√(n))`

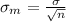
Then the average of the sample will be

`\mu_m = 31\ years`

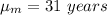
And the standard deviation of the sample will be

`\sigma_m =(10)/(√(10)) = 3.1622`

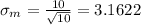
Now we look for the probability that the mean of the sample is greater than or equal to 28.

This is

`P ({\displaystyle{\overline {x}}}\geq 28)`

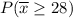
To find this probability we find the Z-score

`Z = (X -\mu)/((\sigma)/(√(n)))`

`Z = (28 -31)/((10)/(√(10))) = -0.95`

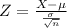
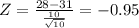
So

`P({\displaystyle{\overline {x}}}\geq 28) = P(\frac{{\displaystyle {\overline {x}}}-\mu}{(\sigma)/(√(n))}\geq(28-31)/((10)/(√(10)))) = P(Z\geq-0.95)`

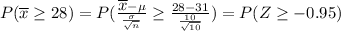
We know that

`P(Z\geq-0.95)=1-P(Z<-0.95)`

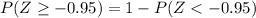
Looking in the normal table we have:

`P(Z\geq-0.95)=1-0.1710\\\\P(Z\geq-0.95) = 0.829`

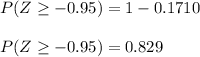
Finally P = 83%