Answer:
P = 73%
Explanation:
We look for the percentage of employees who are not more than 40 years old.
This is:
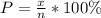
Where x is the number of new employees who are not over 40 years old and n is the total number of new employees.
We do not know the value of x or n. However, the probability of randomly selecting an employee that is not more than 40 years old is equal to
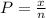
Then we can solve this problem by looking for the probability that a new employee selected at random is not more than 40 years old.
This is:
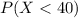
Then we find the z-score
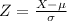
We know that:
μ = 34 years
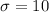 years
years
So
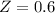
Then
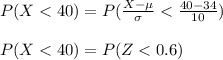
So we have
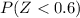
Looking in the normal standard tables:
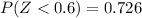
Finally P = 73%