Answer:
P = 21%
Explanation:
We look for the percentage of employees who are not more than 30 years old.
This is:
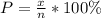
Where x is the number of new employees who are not over 30 years old and n is the total number of new employees.
We do not know the value of x or n. However, the probability of randomly selecting an employee that is not more than 30 years old is equal to
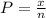
Then we can solve this problem by looking for the probability that a new employee is not more than 30 years old.
This is:

Then we find the z-score

We know that:
μ = 38 years
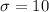 years
years
So
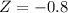
Then
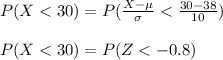
By symmetry of the distribution
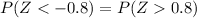
Looking in the normal standard tables

Finally P = 21%