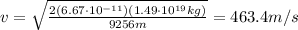Question

A team of astronauts is on a mission to land on and explore a large asteroid. In addition to collecting samples and performing experiments, one of their tasks is to demonstrate the concept of the escape speed by throwing rocks straight up at various initial speeds. With what minimum initial speed ????esc will the rocks need to be thrown in order for them never to "fall" back to the asteroid? Assume that the asteroid is approximately spherical, with an average density ????=4.49×106 g/m3 and volume ????=3.32×1012 m3 . Recall that the universal gravitational constant is ????=6.67×10−11 N·m2/kg2 .

Answer 1

463.4 m/s

Step-by-step explanation:

The escape velocity on the surface of a planet/asteroid is given by

`v=\sqrt{(2GM)/(R)}` (1)

where

G is the gravitational constant

M is the mass of the planet/asteroid

R is the radius of the planet/asteroid

For the asteroid in this problem, we know

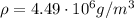`\rho=4.49\cdot 10^6 g/m^3` is the density

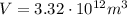`V=3.32\cdot 10^(12) m^3` is the volume

So we can find its mass:

`M=(\rho)/(V)=(4.49\cdot 10^6 g/m^3)(3.32\cdot 10^(12)m^3)=1.49\cdot 10^(19) kg`

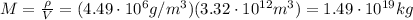
Also, the asteroid is approximately spherical, so its volume is given by

`V=(4)/(3)\pi R^3`

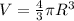
where R is the radius. Solving the formula for R, we find its radius:

`R=\sqrt[3]{(3V)/(4\pi)}=\sqrt[3]{(3(3.32\cdot 10^(12)m^3))/(4\pi)}=9256 m`

So now we can use eq.(1) to find the escape velocity:

`v=\sqrt{(2(6.67\cdot 10^(-11))(1.49\cdot 10^(19)kg))/(9256 m)}=463.4 m/s`