Answer:
c) 3 units
d) g(x) - f(x) = x² + 2x
e) (-∞, -2] ∪ [0, ∞)
Step-by-step explanation:
Part (c)
To calculate the length of FC, first find the coordinates of point C.
The y-value of point C is zero since this is where the function f(x) intercepts the x-axis. Therefore, set f(x) to zero and solve for x:
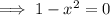
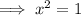
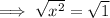

As point C has a positive x-value, C = (1, 0).
To find point F, substitute the x-value of point C into g(x):
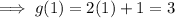
⇒ F = (1, 3).
Length FC is the difference in the y-value of points C and F:
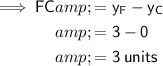
Part (d)
Given functions:
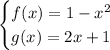
Therefore:
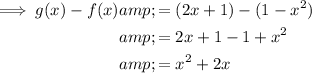
Part (e)
The values of x for which g(x) ≥ f(x) are where the line of g(x) is above the curve of f(x):
Point A is the y-intercept of both functions, therefore the x-value of point A is 0.
To find the x-value of point E, equate the two functions and solve for x:
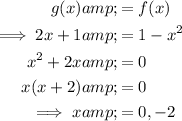
As the x-value of point E is negative ⇒ x = -2.
Therefore, the values of x for which g(x) ≥ f(x) are:
- Solution: x ≤ -2 or x ≥ 0
- Interval notation: (-∞, -2] ∪ [0, ∞)