Answer:
One mass's kinetic energy is 4 times the other.
Explanation:
The formula for kinetic energy is
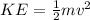
Where
KE is the kinetic energy
m is the mass
v is the velocity
- Now, let mass of the first be m (second is identical so mass of 2nd is m as well)
- Let velocity of the first one be v. Since 2nd one is travelling twice as fast, its velocity will be 2v
KE of 1st mass is:
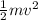
KE of 2nd mass is:
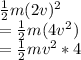
Hence, the kinetic energy of the 2nd mass is 4 times the first.