Question

Helppppppppppppp!!!!!!

Answer 1

There are 17 girls and 5 boys.

Explanation:

Let b and g represent the number of boys and the number of girls respectively.

Then b + g = 22 (students), and g = b + 12.

Substituting b + 12 for g in b + g = 22 yields:

b + (b + 12) = 22

or:

2b + 12 = 22, or 2b = 10, so that b = 5.

Then g = b + 12 = 5 + 12 = 17.

There are 17 girls and 5 boys.

Answer 2

Question 1:

For this case, let the variable "x" be the number of girls in the classroom. Let the variable "y" be the number of boys in the classroom.

We propose the equations:

`x + y = 22\\x = y + 12`

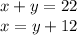
We substitute the second equation in the first:

`y + 12 + y = 22\\2y = 22-12\\2y = 10\\y = 5`

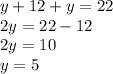
So, in the classroom there are 5 boys.

`x = 5 + 12\\x = 17`

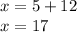
So, there are 17 girls.

Answer:

5 guys

17 girls

Question 2:

For this case we have to:

Let x be the variable that represents the amount of money Jamie has.

Let y the variable that represents the amount of money that Kristen has

We have to:

`x = 2y\\x + y = 36`

We substitute the first equation in the second:

`2y + y = 36\\3y = 36\\y = \frac {36} {3}\\y = 12`

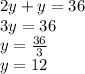
Looking for the value of x:

`x = 2 (12)\\x = 24`

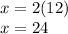
Answer:

So, Jaime you have $ 24 and Kristen you have $ 12.

Question 3:

For this case we have to:

Let "x" be the variable that represents the number of dogs in the Pet Stop.

Let "y" be the variable that represents the number of cats in the Pet Stop.

We have to:

`x + y = 15\\4x = y`

We substitute the second equation in the first:

`x + 4x = 15\\5x = 15\\x = \frac {15} {5}\\x = 3`

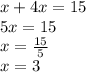
We look for the value of y:

`y = 4x\\y = 4 (3)\\y = 12`

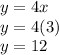
So, there are 12 cats and 3 dogs.

Answer:

12 cats

3 dogs