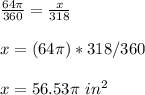Answer:
Part 1) The area of the shaded region is
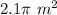
Part 2) The length of the arc AB is
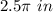
Part 3) The area of the shaded region is
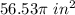
Explanation:
Part 1) Find the area of the shaded region
step 1
Find the area of the circle
The area is equal to
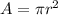
we have
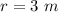
substitute
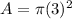
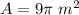
step 2
we know that
The area of complete circle subtends a central angle of 360 degrees
so
by proportion
calculate the area of the shaded region with a central angle of 84 degrees
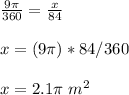
Part 2) What is the length of arc AB?
step 1
we know that
The circumference of a circle is equal to
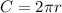
we have
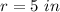
substitute
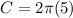
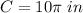
step 2
we know that
The length of complete circle subtends a central angle of 360 degrees
so
by proportion
calculate the length of the arc AB with a central angle of 90 degrees
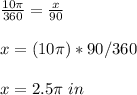
Part 3) Find the area of the shaded region given that XY measures 8 in
step 1
Find the area of the circle
The area is equal to
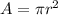
we have
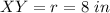
substitute
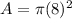
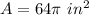
step 2
we know that
The area of complete circle subtends a central angle of 360 degrees
so
by proportion
calculate the area of the shaded region with a central angle of (360-42)=318 degrees