Answer:
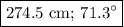
Explanation:
If we open the surface of the pole and lay it flat, we will get a rectangle with the red stripe as a diagonal.
l = 260 cm.
The width of the rectangle is enough for two revolutions (i.e., twice the circumference).
w = 2C = 2 × 2πr = 4π × 14/2 = 28π cm = 87.96 cm
Length of stripe
The stripe is the diagonal of the rectangle.
d² = 260² + (28π)² = 67 600 + 87.96² = 67 600 + 7738 = 75 338
d = √(75 338) = 274.5 cm
Angle with horizontal
tanθ = 260/(28π) = 260/87.96 =2.956
θ = arctan2.956
θ = 71.3°
The stripe is
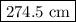 long and the angle with the horizontal is
long and the angle with the horizontal is
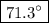 .
.