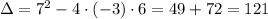Question

Need help fast due today thanks

Answer 1

1

Move everything to the left by subtracting 25 from both sides:

`81x^2-25=0`

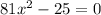
Both terms are squares:
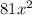`81x^2` is the square of
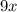`9x`, while 25 is the square of 5. So, we can apply the factoring

`a^2-b^2=(a+b)(a-b)`

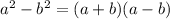
To factor the expression as

`(9x+5)(9x-5)=0`

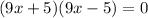
A multiplication is zero if and only if one of the factors is zero, so we have

`(9x+5)(9x-5)=0 \iff 9x+5=0 \lor 9x-5=0 \iff x=-(5)/(9) \lor x=(5)/(9)`

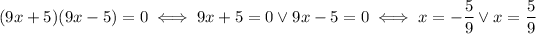
2

The discriminant of the quadratic expression
`ax^2+bx+c` is defined as

`\Delta = b^2-4ac`

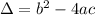
So, you have

`\Delta = 0^2-4\cdot(-1)\cdot(-25) = -100`

3

Similarly, we have

`\Delta = 7^2-4\cdot(-3)\cdot 6 = 49+72=121`