Question

how much would you need to deposit in an account now in order to have 6000 in the account in 8 years. assume the account earns 6% interest compounded monthly

Answer 1

$3,717.14

Explanation:

Compound interest is the interest on the principal funding as well as the interest itself.

Compound Interest Formula

Compound interest can be solved by plugging known values into a formula.

• 
  `A = P(1 + (r)/(n))^(nt)`

In this formula, the variables stand for different values.

• A = total amount
• P = principal amount
• r = rate as a decimal
• n = times compounded per time period
• t = time

So, for this question, we can plug in the values we are given and solve for P.

Identifying Known Values

First, let's find the exact numbers we are going to plug in.

• 6000 is the final amount we want, so A = 6000.
• 6%, the rate, is 0.06 as a decimal, so r = 0.06.
• Since interest is compounded each month per year, n = 12.
• The total time is 8 years, so t = 8.

Solving For P

Now we can plug all of these values in.

• 
  `6000=P(1+(0.06)/(12))^(12*8)`

First, simplify the values within the parentheses and in the exponent through arithmetic.

• 
  `6000 = P(1.005)^(96)`

Next, divide both sides by
`1.005^(96)`

• 3717.14 ≈ P

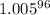
*Note that the answer has been rounded to the nearest hundredth.

This means that you would need to deposit $3,717.14 into the account to have $6,000 in 8 years.