Answer:
The values of k are 2/3 and -1
Explanation:
Product of zeros = αβ= constant / coefficient of x^2 = 4/k
Sum of zeros =α+β = - coefficient of x / coefficient of x^2= -4/k
Given
Consider a= α and b= β
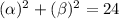
 can be written as
can be written as
 if we add
if we add
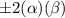 in the above equation.
in the above equation.
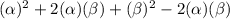
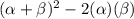
Putting values of αβ and α+β
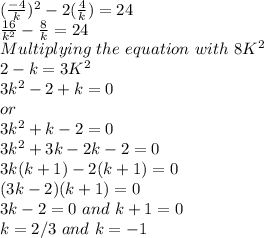
The values of k are 2/3 and -1