Answer: a= 16
Explanation:
We have the following expression:
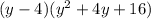
To find the value of the coefficient "a" you must use the distributive property to multiply the expression:
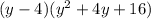
until you transform it to the form:
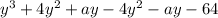
Then we have
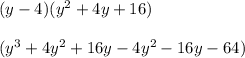
Therefore the value of a in the polynomial is 16