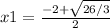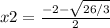Answer:
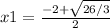
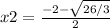
Explanation:
To find the zeros of the quadratic function f(x)=6x^2 + 12x – 7 we need to factorize the polynomial.
To do so, we need to use the quadratic formula, which states that the solution to any equation of the form ax^2 + bx + c = 0 is:
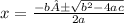
So, the first thing we're going to do is divide the whole function by 6:
6x^2 + 12x – 7 = 0 -> x^2 + 2x - 7/6
This step is optional, but it makes things quite easier.
Then we using the quadratic formula, where:
a=1, b= 2, c = -7/6.
Then:
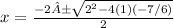
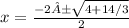

So the zeros are: