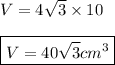Answer:
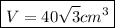
Explanation:
A prism is a solid object having two identical bases, hence the same cross section along the length. Prism are called after the name of their base. In a right prism every edge that connects the base and the opposite face makes right angles with both faces. Moreover, a triangular prism is a solid whose base is a triangle. In general, a prism's volume is always equal to the area of its base, which has the same area of the top face, times its height. In mathematical language:

Since the base is an equilateral triangle with side 4 cm, then we'll use Heron's formula to find the area. This formula uses triangle's side lengths and the semiperimeter. A polygon's semiperimeter s is half its perimeter. So the area of a triangle can be found by
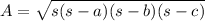 being
being
 the corresponding sides of the triangle. So:
the corresponding sides of the triangle. So:
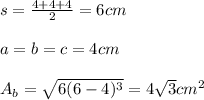
Finally: