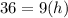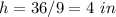Question

A cylinder and a cone have the same volume. The cylinder has a radius of 2 inches and a height of 3 inches . The cone has a radius of 3 inches. What is the height of the cone ?

Answer 1

The height of the cone is
`4\ in`

Explanation:

step 1

Find the volume of the cylinder

The volume of the cylinder is equal to

`V=\pi (r)^(2)(h)`

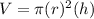
substitute the values

`V=\pi (2)^(2)(3)=12\pi\ in^(3)`

step 2

Find the height of the cone

The volume of the cone is equal to

`V=(1/3)\pi (r)^(2)(h)`

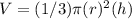
Remember that the volume of the cone is equal to the volume of the cylinder

substitute the given values and solve for h

`12\pi=(1/3)\pi (3)^(2)(h)`

Simplify

`36=9(h)`

`h=36/9=4\ in`