Answer:
The correct option is A.
Explanation:
An organization consists of 8,684 employees. The organization surveyed 884 of their employees and found that 36% of those surveyed disliked the new vacation policies. It means
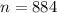
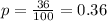
The value of z-score for 95% confidence level is 1.96.
The formula for margin of error is
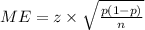
Where, z is z-score at given confidence level, p is sample proportion and n is number of samples.
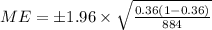
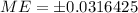
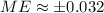
The margin of error is ±0.032 and the sample size is appropriately large. Therefore, the correct option is A.