Answer:
D
Explanation:
The arcsine (
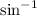 ) function of x is defined as the inverse sine function of x when -1≤x≤1.
) function of x is defined as the inverse sine function of x when -1≤x≤1.
So, when
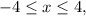
we have that
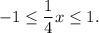
This gives us the domain
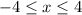 of the function
of the function
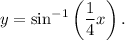
The range of the function
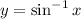 is
is
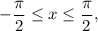 so the range of the function
so the range of the function
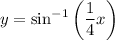 is the same (options A and C are false).
is the same (options A and C are false).
When x=-4,
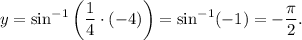
So, option B is false and option D is true.