Answer:
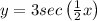
Explanation:
The graphs of
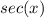 can be obtained from the graph of the cosine function using the reciprocal identity, so:
can be obtained from the graph of the cosine function using the reciprocal identity, so:

But in this problem, the graph stands for the function:
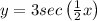
Because the period is now 4π as indicated and for
 in the figure and this can be proven as follows:
in the figure and this can be proven as follows:
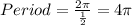
Also,
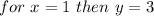 as indicated in the figure and this can be proven as:
as indicated in the figure and this can be proven as:
