Answer:
The solution is:
Part A.
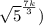 which is sqrt(5)^7k/3[/tex]
which is sqrt(5)^7k/3[/tex]
Part B. k = 18/7
Explanation:
Part A.
To solve this part, we're going two use THREE important properties of exponents:
1.
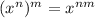
2.
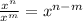
3.
![\sqrt[n]{x^(m)} = x^{(m)/(n) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/obzf6o0rlmuwbg8ir6ilvket6lu5d5zaiz.png)
Let's work the numerator using the properties 1, 2 and 3:
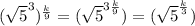
Let's work the denominator using the properties 1, 2 and 3:

Now dividing the numerator by the denominator:
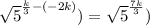
Part B
if
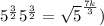
Then:

So
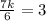
Solving for k, we have:
k = 18/7