Question

If logM/N = 4 and logP/N =7, what can you say about the relationship between M and P?

A. P= 3M
B. M= 3P
C. P= 1000M
D. P= 100M

Answer 1

C. P= 1000M

Explanation:

`log((M)/(N) )=4`

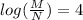
Using the quotient rule of logs we can write:

log(M) - log(N) = 4

or

log(M) - 4 = log(N) (Equation 1)

`log((P)/(N) )=4`

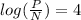
Using the quotient rule of logs we can write:

log(P) - log(N) = 7

or

log(P) - 7 = log(N) (Equation 2)

Comparing equation 1 and 2, we can write:

log(M) - 4 = log(P) - 7

-4 + 7 = log(P) - log(M)

log(P) - log(M) = 3

`log((P)/(M) )=3`

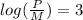
Converting the log to exponential form we get:

`(P)/(M)=10^(3)\\\\(P)/(M)=1000\\\\P=1000M`

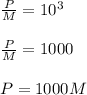
Thus, option C gives the correct answer.