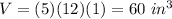Question

A pack of folders has a length of 5 inches, a width of 12 inches, and a height of 1 inch. The pack of folders will be shipped in a box that holds 12 packs of folders. Which statements are true?

Select all statements that are true.

A) Each pack of folders has a volume of 60 cubic inches.
B) The box has a volume of about 720 cubic inches.
C) If the box held 15 packs of folders, it would have a volume of about 1,200 cubic inches.
D) If the box help 20 packs of folders, it would have a volume of about 1,200 cubic inches.
E) Each pack of folders has a volume of 24 cubic inches.

Answer 1

A) Each pack of folders has a volume of 60 cubic inches.

B) The box has a volume of about 720 cubic inches

D) If the box help 20 packs of folders, it would have a volume of about 1,200 cubic inches.

Explanation:

Verify each statement

A) Each pack of folders has a volume of 60 cubic inches.

The statement is True

Because

The volume of each pack of folders is equal to

`V=(5)(12)(1)=60\ in^(3)`

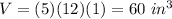
B) The box has a volume of about 720 cubic inches

The statement is True

Because

The volume of the box is equal to the volume of one pack of folders multiplied by 12

so

`V=(12)60=720\ in^(3)`

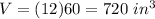
C) If the box held 15 packs of folders, it would have a volume of about 1,200 cubic inches

The statement is False

Because

Applying proportion

`(12)/(720)(packs)/(in^(3))=(15)/(x)(packs)/(in^(3))\\ \\x=720*15/12\\ \\x=900\ in^(3)`

`900\ in^(3)\\eq 1,200\ in^(3)`

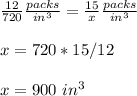
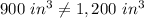
D) If the box help 20 packs of folders, it would have a volume of about 1,200 cubic inches.

The statement is True

Because

Applying proportion

`(12)/(720)(packs)/(in^(3))=(20)/(x)(packs)/(in^(3))\\ \\x=720*20/12\\ \\x=1,200\ in^(3)`

`1,200\ in^(3)= 1,200\ in^(3)`

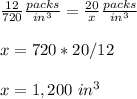
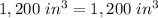
E) Each pack of folders has a volume of 24 cubic inches.

The statement is False

Because

The volume of each pack of folders is equal to

`V=(5)(12)(1)=60\ in^(3)`