Answer:
Vertex = (4, 9)
The vertex is the maximum
Explanation:
The vertex form of a quadratic of the form
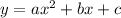 is
is
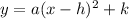 where
where
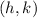 are the coordinates of the vertex.
are the coordinates of the vertex.
Comparing the vertx form of the quadratic to our quadratic
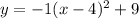 , we can infer that
, we can infer that
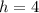 and
and
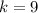 , so its vertex is the point (4, 9).
, so its vertex is the point (4, 9).
Now, in a parabola of the form
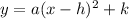 if
if
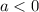 the parabola open downwards and the vertex is its maximum, and if
the parabola open downwards and the vertex is its maximum, and if
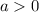 the parabola open upwards and the vertex is its minimum.
the parabola open upwards and the vertex is its minimum.
We know from our parabola that
 . Since
. Since
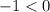 , the vertex of our parabola is its maximum.
, the vertex of our parabola is its maximum.
We can conclude that the vertex of our parabola is (4, 9) and is its maximum.