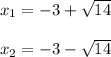Question

Solve for x use the completing the square method x^2+6x=5

Answer 1

x=−3±√14

Hope this helps!

Answer 2

`x_(1) =-3 +√(14) \\\\x_(2) =-3 -√(14)`

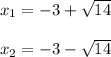
Explanation:

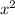`x^(2)`+6x-5=0

we divide the coefficient of the X by half :

in this case: 6/2 = 3 , then we do the following

The result obtained is raised to square power: 3^2=9

we sum and subtract by 9 to maintain the balance of the equation:

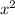`x^(2)`+6x+9-9-5=0

we have:

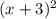`(x+3)^(2)`-9-5=0

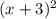`(x+3)^(2)` = 14

lets apply square root on both sides of the equation:

`\sqrt{(x+3)^(2)}=√(14)`

we know:

`\sqrt{a^(2)} = abs(a)`

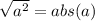
so we have:

abs(x+3)=
`√(14)`

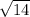
from where two solutions are obtained

`x_(1) + 3 =√(14) \\\\x_(2) + 3 =-√(14)`

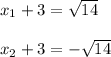
finally we have:

`x_(1) =-3 +√(14) \\\\x_(2) =-3 -√(14)`