Hello!
The answer is:
The range of the function is:
Range: (0,1000]
Why?
To know the range of this function in this context, first, we need to find which is the maximum value that the function can reach.
It's true that exponential function has a range which comprehends all the real numbers greater than 0, but for the experiment, the range of the function will be all the numbers greater than 0 but less or equal than the highest value that the population of bacteria at the start of the experiment.
So, to calculate the highest population of bacteria before even it started to decrease, we need to use "t" equal to 0.
Calculating we have:
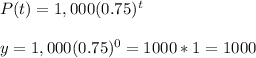
Hence, we have that the maximum value that the function can reach is 1000 units of bacteria. Meaning that the range of the function will be:
Range: (0,1000]
Have a nice day!