Question

Wrote the equation of a line that includes the point (22,12) and has a slope of 4 in standard form.

Answer 1

Hello!

The answer is:

The standard form of a line that includes the point (22,12) and has a slope of 4, is:

`-4x+y=-76`

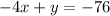
Why?

To solve this problem, we need to remember the standard form of the line which is:

`Ax+By=c`

So, we are asked to find and write the equation of a line that includes the point (22,12) and has a slope of 4 (positive), in standard form. We know that the slope of a line is the coefficient of the linear term "x".

We need to write the equation in the point-slope form in order to find the standard form.

The point-slope form of the line is equal to:

`y-y_(1)=m(x-x_(1))`

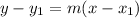
We are given the point (22,12) and slope of 4.

Where,

`x_(1)=22\\y_(1)=12`

Then, substituting the given information into the point-slope equation, we have:

`y-12=4(x-22)\\\\y-12=4x-88\\\\y-4x=-88+12\\\\-4x+y=-76`

So, the correct answer is the last option, the standard form of a line that incluides the point (22,12) and has a slope of 4, is:

`-4x+y=-76`

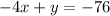
Have a nice day!

Answer 2

`- 4x + y = - 76`

Step-by-step explanation

We use the formula,

`y-y_1=m(x-x_1)`

where

`x_1=22`

`y_1=12`

m=4

We substitute the values into the formula to get,

`y - 12 = 4(x - 22)`

`y - 12 = 4x - 88`

y=4x-88+12

`y = 4x - 76`

In standard form, the equation is:

`- 4x + y = - 76`