Hello!
The answer is:
The third option,
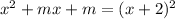
Why?
We are looking for an equation that establishes a relationship between the perfect-square trinomial and the givens notable products.
So, we are looking for a notable product that gives us a value of "m" that is the coefficient of the linear term (x) and it's also the constant term.
- Trying with the two first options, we have:
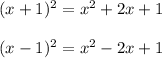
We can see that for these first two options, the value of m has not the same value for the coefficient of the linear term and the constant term since m is equal 2 and the constant number is not 2.
- Trying with the third option, we have:
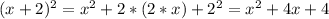
Now, we can see that the value of m is the same for the coefficient of the linear term and the constant term, we can see that m is equal to 4.
So, the correct option is the third option, because

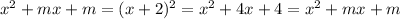
Have a nice day!