Question

The quadrilateral ABCD on a coordinate plane has the following characteristics.

AD can be represented by the equation y = =3x where -1
BC can be represented by the equation y = =3x + 11 where 2
CD has coordinates C(2,5) and D(-1,3)
In order for ABCD to be a parallelogram, which coordinates correspond to AB?

Answer 1

Answer with explanation:

Property of Quadrilateral A B CD

⇒Equation of Line AD is, y= -3 x.

⇒Equation of Line BC is, y= -3 x +11

Coordinates of CD = C(2,5) and D(-1,3)

Equation of line CD will be

`(y-5)/(x-2)=(3-5)/(-1-2)\\\\-3 * (y-5)=-2* (x-2)\\\\-3 y +15=-2 x +4\\\\2 x -3 y +11=0`

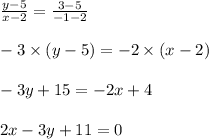
Equation of line AB will be, which is parallel to CD, as opposite sides of parallelogram are parallel and equal,is equal to

2 x -3 y + k=0

Because when lines are parallel their slopes are equal.

→→Equation of line AD is , y= - 3 x.

Coordinates of point A can be calculated by

→2 x -3 × (-3 x ) +k=0

→2 x +9 x +k=0

`\rightarrow x=(-k)/(11)\\\\\rightarrow y=(3k)/(11)`

→→→Similarly, Coordinate of point D can be calculated by solving these two lines:

y = -3 x + 11

2 x -3 y + k=0

→2 x -3 × (-3 x +11) +k=0

→2 x +9 x -33 +k=0

→11 x =33 -k

`x=(33-k)/(11)`

`y=-3 * (33-k)/(11)+11\\\\y=(-99+3 k+121)/(11)\\\\y=(22+3 k)/(11)`

→→Coordinates of A is
`((-k)/(11),(3k)/(11))`

Coordinates of Point D is
`((33-k)/(11),(22+3k)/(11))`.

you, can get infinite number of ordered pairs, for different value of k.

For, k=0 ,

A= (0,0)

D=(3,2)