Question

What are the amplitude, period, and phase shift of the given function?
f(t)= -1/2 sin (3t-2π)

Answer 1

c.

Explanation:

amplitude:1/2

phase shift: 2/3 pi

period: 2/3 pi

Answer 2

C

Explanation:

For a sine/cos function given in the form f(x) = A sin (Bx+C) , we can say:

|A| is the amplitude

2π/B is the period, and

-C/B is the phase shift

For the function given
`f(t)=-(1)/(2)sin(3t-2\pi)`

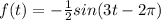
A =
`(1)/(2)`

B = 3

C = -2π

Using the information given, we can find:

Amplitude is
`|-(1)/(2)|\\=(1)/(2)`

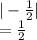
Period is
`(2\pi)/(3)`

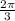
Phase Shift is
`-(-2\pi)/(3)\\=(2\pi)/(3)`

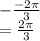
Hence, the correct answer choice is C