Answer:
(8,0)
Explanation:
The equation that models the path traced by the ball is
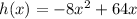
To find the point at which the ball hit the ground, we must equate the function to zero.

Factor;
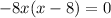
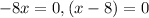
This implies that;
x=0,x=8,
At x=0, the ball was not yet kicked.
So we take x=8, to be the time the ball hit the ground.
We substitute x=8 into the function to get;
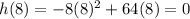
Hence the point at which the ball hit the ground is (8,0)