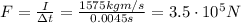Question

After the cable snaps and the safety system fails, an elevator cab free-falls from a height of 31 m. During the collision at the bottom of the elevator shaft, a 90 kg passenger is stopped in 4.5 ms. (Assume that neither the passenger nor the cab rebounds.) (a) What is the magnitude of the impulse on the passenger during the collision? N · s (b) What is the magnitude of the average force on the passenger during the collision? N Suppose the passenger were to jump upward with a speed of 7.1 m/s relative to the cab floor just before the cab hits the bottom of the shaft. Assume the same stopping time as above. (c) What is the magnitude of the impulse on the passenger during the collision? N · s (d) What is the magnitude of the average force on the passenger during the collision? N

Answer 1

(a) 2214 kg m/s

First of all, we need to find the speed of the passenger just before hitting the ground. This can be found by using the law of conservation of energy: in fact, the initial gravitational energy of the passenger is all converted into kinetic energy as he falls down:

`mgh=(1)/(2)mv^2`

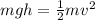
where

m = 90 kg is the mass of the passenger

g = 9.8 m/s^2 is the acceleration due to gravity

h = 31 m is the initial height

v is the final speed of the passenger

Solving the equation for v,

`v=√(2gh)=√(2(9.8 m/s^2)(31 m))=24.6 m/s`

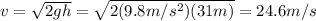
Now we can find the impulse, which is equal to the change in momentum of the passenger:

`I=\Delta p = m\Delta v = (90 kg)(0-24.6 m/s)=-2214 kg m/s`

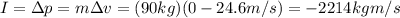
And the negative sign means the impulse is in the opposite direction to the motion of the passenger.

(b)
`4.92\cdot 10^5 N`

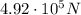
The magnitude of the impulse is equal to the product between the average force, F, and the time of the collision,
`\Delta t`

`I=F\Delta t`

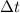
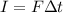
Since we know

I = 2214 kg m/s (impulse)

t = 4.5 ms = 0.0045 s (time of the collision)

We can solve the formula to find the average force, F:

`F=(I)/(\Delta t)=(2214 kg m/s)/(0.0045 s)=4.92\cdot 10^5 N`

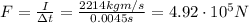
(c) 1575 kg m/s

In this case, the passenger jumps upward with a speed of 7.1 m/s relative to the cab floor just before hitting the ground. Since the cab floor is moving with a speed of 24.6 m/s downward, the velocity of the passenger relative to the ground is

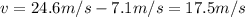`v=24.6 m/s - 7.1 m/s=17.5 m/s` (downward)

So this time the impulse will be:

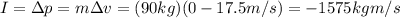
`I=\Delta p = m\Delta v = (90 kg)(0-17.5 m/s)=-1575 kg m/s`

(d)
`3.5\cdot 10^5 N`

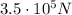
This part of the problem can be solved as part b). The magnitude of the impulse is equal to the product between the average force, F, and the time of the collision,
`\Delta t`

`I=F\Delta t`

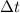
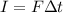
Since we know

I = 1575 kg m/s (impulse)

t = 4.5 ms = 0.0045 s (time of the collision)

We can solve the formula to find the average force, F:

`F=(I)/(\Delta t)=(1575 kg m/s)/(0.0045 s)=3.5\cdot 10^5 N`