Question

Tiffany kicks a soccer ball off the ground and in the air, with an initial velocity of 28 feet per second. Using the formula H(t) = −16t2 + vt + s, what is the maximum height the soccer ball reaches?15.6 feet14.1 feet13.5 feet12.3 feet

Answer 1

Answer: the answer is 12.3

Step-by-step explanation:

i took the test

Answer 2

The maximum height of soccer ball is 12.25 ft.

Step-by-step explanation:

You know: H(t) = −16t² + vt + s

First you must know the value of the constant "s". For this you know that at the beginning, at time t = 0, the initial height H (0) is zero. Also, you know that the speed v is 28 feet per second. So:

H(0)=-16*0² + 28*0 + s

0=-16*0² + 28*0 + s

0=s

Then, the speed expression is determined as:

H(t) = −16t² + 28*t

The vertex is a point that is part of the parabola, which has the value as ordered minimum or maximum function. At that point an imaginary axis can be drawn that makes symmetric the graph of the function, which is called the axis of symmetry.

Being the parabola: f(x)=a*x² + b*x + c

the vertex is calculated as:
`(x,y)=((-b)/(2*a) ,f((-b)/(2*a)))`

In this case, the point "x" of the vertex indicates the time at which the soccer ball reaches the maximum "y" height ( The vertex is at a maximum point of the function.) So, being a=-16 and b=28, the vertex is:

`x=(-b)/(2*a) =(-28)/(2*(-16))`

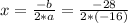
x=0.875

H(0.875)=-16*(0.875)²+28*(0.875)=12.25

The maximum height of soccer ball is 12.25 ft.