Answer:
35.25
Explanation:
There are 4 data:
262, 313, 393, and 323
The formula for MAD (mean absolute deviation) =
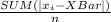
Where x_i are the each individual values (stated)
XBar is the average value
n is the number of data
First, let's find XBar, or the average. We add up all the 4 numbers and divide by 4 to get:
XBar = (262+313+393+323)/4=322.75
Now, let's calculate MAD:
MAD =
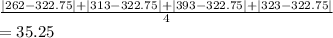
MAD = 35.25