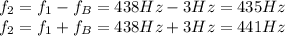Answer:
It is producing either a 435-Hz sound or a 441-Hz sound.
Step-by-step explanation:
When two sound of slightly different frequencies interfere constructively with each other, the resultant wave has a frequency (called beat frequency) which is equal to the absolute value of the difference between the individual frequencies:
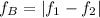 (1)
(1)
In this problem, we know that:
- The frequency of the first trombone is
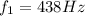
- 6 beats are heard every 2 seconds, so the beat frequency is
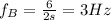
If we insert this data into eq.(1), we have two possible solutions for the frequency of the second trombone: