Question

What is the arc length when theta = 2pi/3 and the radius is 8 cm

Answer 1

Answer: The measure of arc length = 16.74

Explanation:

Since we have given that

Angle =
`(2\pi )/(3)`

Radius = 8 cm

We need to find the arc length.

As we know the formula for "Arc length":

`l=r\theta\\\\l=8* (2\pi )/(3)\\\\l=8* (2* 3.14)/(3)\\\\l=16.74`

Hence, the measure of arc length = 16.74

Answer 2

The arc length is 16.76 cm.

Explanation:

Given that,

Arc length = l = ?

Angle = theta =
`(2\pi)/(3)`

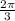
Radius = r = 8 cm

The relation between the arc length (l), angle (theta) and radius (r) is calculated using
`l = r * \theta`

By putting values in the above relation, we get

`l = (2\pi)/(3) * 8`

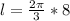
l ≈ 16.76 cm

Therefore, the arc length is 16.76 cm.