Question

The lowest pressure attainable using the best available vacuum techniques is about 10^−12 N/m^2.

At such a pressure, how many molecules are there per cm^3 at 19 °C?

Answer 1

247 molecules

Step-by-step explanation:

This problem can be solved by using the ideal gas equation:

`pV=nRT`

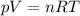
where in this case we have

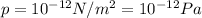`p=10^(-12)N/m^2 = 10^(-12) Pa` is the lowest pressure attainable

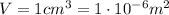`V=1 cm^3 = 1\cdot 10^(-6)m^2` is the volume we are considering

n is the number of moles

R is the gas constant

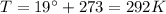`T=19^(\circ)+273=292 K` is the absolute temperature

Solving the equation for n, we find

`n=(pV)/(RT)=((10^(-12) Pa)(1\cdot 10^(-6)m^3))/((8.314 J/mol K)(292 K))=4.1\cdot 10^(-22)mol`

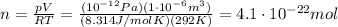
And since the number of molecules in 1 mole of gas is

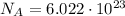`N_A = 6.022\cdot 10^(23)` (avogadro number)

The number of molecules present here is

`N=n N_A = (4.1\cdot 10^(-22)mol)(6.022 \cdot 10^(23) mol^(-1))=246.9 \sim 247`

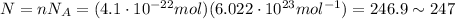
so, there are approximately 247 molecules.