Remember that row operations don't affect the determinant:
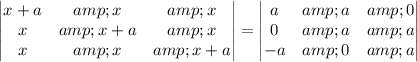
(that is, subtract row 2 from row 1; subtract row 3 from row 2; and subtract row 1 from row 3. This is not the only way to do it, of course.)
Factoring out
 gives
gives
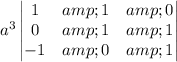
Notice that adding rows 1 and 3 gives the same numbers in row 2. In other words, the rows are not linearly independent, which means the matrix is singular, and this is so for any value of
 .
.