Question

It appears that people who are mildly obese are less active than leaner people. One study looked at the average number of minutes per day that people spend standing or walking. Among mildly obese people, the mean number of minutes of daily activity (standing or walking) is approximately Normally distributed with 376 minutes and standard deviation 64 minutes. The mean number of minutes of daily activity for lean people is approximately Normally distributed with 528 minutes and standard deviation 107 minutes. A researcher records the minutes of activity for an SRS of 7 mildly obese people and an SRS of 7 lean people. (a) What is the probability that the mean number of minutes of daily activity of the 7 mildly obese people exceeds 400 minutes? (Enter your answer rounded to four decimal places.)

Answer 1

0.1611

Explanation:

For the distribution of sample means, we use the z score formula

`z=\frac{\bar{X}-\mu}{\sigma / √(n)}`

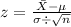
For this problem, the mean, μ, is 376 and the standard deviation, σ, is 64. Our sample size, n, is 7.

We want P(X > 400):

z = (400-376)/(64÷√7) = 24/(64÷2.6458) = 24/24.1893 = 0.99

Looking up this value in a z chart, we see that the area under the curve to the left of this is 0.8389. However, we want the area to the right; this means we subtract from 1:

1-0.8389 = 0.1611