Question

What are the equations of the asymptotes of the graph of the function f(x)=3x^2-2x-1/x^2+3x-10

Answer 1

Vertical asymptotes

`x = -5\\\\x = 2`

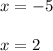
Horizontal asymptote

`y=3`

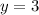
Explanation:

We have the function
`f(x) = (3x ^ 2-2x-1)/(x ^ 2 + 3x-10)` and we want to find its asymptotes.

First we find their vertical asymptotes.

To do this we must factor the denominator of the expression.

`x ^ 2 + 3x-10`

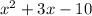
We must look for two numbers that when adding them obtain 3, and when multiplying those same numbers, obtain -10.

The searched numbers are 5 and -2

Then the factors are:

`(x + 5)(x-2)\\\\x ^ 2 + 3x-10 = (x + 5)(x-2)`

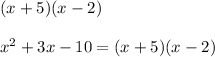
Since the division between zero is not defined then when x tends to -5 the function tends to infinity and when x tends to 2 the function tends to infinity.

So the vertical asymptotes will be the straight lines:

`x = -5\\\\x = 2`

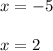
The horizontal asymptote is calculated as:

`\lim_(x \to\infty)f(x)\\\\= \lim_(x \to\infty)(3x ^ 2-2x-1)/(x ^ 2 + 3x-10)`

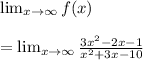
The highest exponent of the function is 2. Then the terms with exponents less than 2 tend to zero

`\lim_(x \to\infty)(3x ^ 2-2x-1)/(x ^ 2 + 3x-10) =\lim_(x \to\infty)(3x ^ 2)/(x ^ 2)\\\\ = \lim_(x \to\infty)(3)/(1) = 3\\\\`

Then

`\lim_(x \to\infty)f(x)=3`

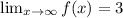
Therefore the horizontal asymptote is:

`y=3`

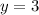
Observe the attached image