Question

An object is launched from a launching pad 208 ft. above the ground at a velocity of 192ft/sec. what is the maximum height reached by the rocket?

Answer 1

The maximum height is 784 feet

Explanation:

In this problem we use the kinematic equation of the height h of an object as a function of time

`h(t) = -16t ^ 2 + v_0t + h_0`

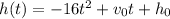
Where
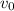`v_0` is the initial velocity and
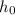`h_0` is the initial height.

We know that

`v_0 = 192\ (ft)/(sec)`

`h_0 = 208\ ft.`

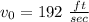
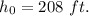
Then the equation of the height is:

`h(t) = -16t ^ 2 + 192t +208`

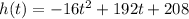
For a quadratic function of the form
`ax ^ 2 + bx + c`

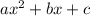
where
`a <0`

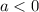
the maximum height of the function is at its vertex.

The vertice is

`x = -(b)/(2a)\\\\y = f((-b)/(2a))`

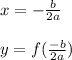
In this case

`a = -16\\b = 192\\c = 208`

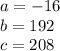
Then the vertice is:

`t = -(192)/(2(-16))\\\\t = 6\ sec`

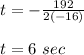
Now we calculate h (6)

`h(6) = -16(6) ^ 2 +192(6) +208\\\\h(6) = 784\ feet`

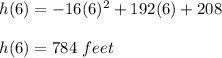
The maximum height is 784 feet