Answer:
8
Explanation:
This question is asking you to solve for the following system of equations, let x be width and y be height of the rectangle.
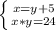
Since the former is already equal to x lets set the second equation to x
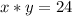
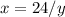
Now we have the following system of equations:
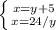
Now that the two equations are equal, we can solve for y:
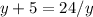
Divide both sides by y
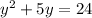
Subtract 24 from the right side setting it to 0:

Solve for y using quadratic formula:
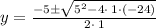
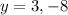
Given the y-values lets plug them into our original equations to find the intersections.
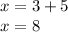
Giving intersection vector (8,3)
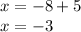
Giving intersection vector (-3,-8)
Since both the width and length of the rectangle must be positive lets use the first vector (8,3) as our solution.
The x value being 8 means the width must be 8, y value being 3 the height must be 3, these variable correlate to our original definitions of making the x value equal to the width of the carpet and y value the height of the carpet.