Question

If the height of the triangle is 3 units more than the base, select the function that represents the area of the triangle.


`A.\\A(b) = (1)/(2) b^(2) + 3\\\\B.\\A(b) = 2bx^(2) + 3\\\\C.\\A(b) = (1)/(2) (b^(2) + 3b)\\\\D.\\A(b) = bx^(2) + 3b`

Answer 1

For this case we have that by definition, the area of a triangle is given by:

`A = \frac {1} {2} * b * h`

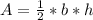
Where:

h: It's the height of the triangle

b: It is the base of the triangle.

They tell us that the height of the triangle is 3 units more than the base. That means that if the base is "b" then the height is "b + 3". So, the area is:

`A(b) = \frac {1} {2} * b * (b + 3)\\A(b) = \frac {1} {2} * b ^ 2 + 3b\\A(b) = \frac {b ^ 2 + 3b} {2}`

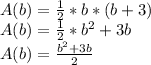
ANswer:

Option C