Answer:
a. Sketch is given in the attachment
b.
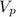 = (0,-525)
= (0,-525)
c.
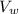 = (
= (
 ,
,
 )
)
d.
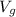 = (60
= (60
 , 60
, 60
 - 525)
- 525)
e. Actual Speed = |
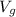 | = 448.3 MPH
| = 448.3 MPH
Direction = Ф = - 79.1°
Direction = Ф = 280.9° with respect to x - axis.
Explanation:
a. Sketch the scenario on the x-y axis.
Where,
Velocity of the plane relative to air =
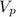
Velocity of the jet stream =
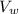
Velocity of the plane relative to ground =
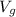
Solution:
Note: Solution is given in the attachment. Please refer to the attachment for the sketch.
b. Express the velocity of the plane relative to the air as a vector.
Solution:
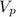 = |
= |
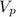 | cosФi + |
| cosФi + |
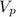 | sinФj
| sinФj
where,
|
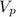 | = magnitude of the vector.
| = magnitude of the vector.
|
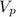 | = 525 MPH
| = 525 MPH
Ф = 270° w.r.t to x - axis. (See the sketch in the attachment)
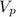 = |
= |
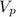 | cosФi + |
| cosФi + |
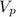 | sinФj
| sinФj
Plug in the values into this equation to express it in the vector form as required.
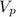 = (525) cos270i + (525) sin270j
= (525) cos270i + (525) sin270j
As, Cos270 = 0
and
Sin270 = -1
So,
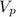 = (525) (0)i + (525) (-1)j
= (525) (0)i + (525) (-1)j
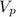 = 0i -525j
= 0i -525j
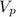 = (0,-525)
= (0,-525)
c. Express the velocity of the jet stream as a vector.
Solution:
Velocity of the jet stream as a vector.
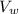 = |
= |
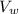 | cosФi + |
| cosФi + |
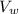 | sinФj
| sinФj
where,
|
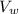 | = magnitude of the vector.
| = magnitude of the vector.
|
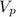 | = 120 MPH
| = 120 MPH
Ф = 45° (See the sketch in the attachment)
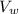 = |
= |
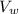 | cosФi + |
| cosФi + |
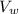 | sinФj
| sinФj
Plug in the values into this equation to express it in the vector form as required.
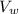 = (120) cos45i + (120) sin45j
= (120) cos45i + (120) sin45j
As, Cos45 =
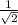
and
Sin45 =
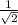
So,
 = (120) (
= (120) (
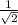 )i + (120) (
)i + (120) (
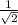 )j
)j
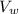 = 60
= 60
 i +60
i +60
 j
j
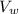 = (
= (
 ,
,
 )
)
d. Find the velocity of the plane relative to the ground.
Solution:
Velocity of the plane relative to the ground = Sum of velocity of plane relative to the air and velocity of the jet stream
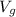 =
=
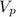 +
+
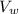
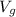 = 0i -525j + 60
= 0i -525j + 60
 i +60
i +60
 j
j
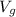 = 60
= 60
 i + 60
i + 60
 - 525j
- 525j
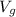 = (60
= (60
 , 60
, 60
 - 525)
- 525)
e. Find the actual speed and direction of the plane relative to the ground. Round to the tenths.
Solution:
Actual Speed = |
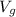 | = magnitude of the velocity of the plane relative to the ground.
| = magnitude of the velocity of the plane relative to the ground.
Actual Speed = |
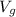 | =
| =

Actual Speed = |
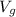 | = 448.3 MPH
| = 448.3 MPH
Direction = Ф =
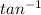 (
(
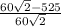 )
)
Direction = Ф = - 79.1°
To find out the direction with respect to x - axis.
Direction = Ф = 360 - 79.1
Direction = Ф = 280.9°