Question

Which of the following pairs of lines are perpendicular? Select all that apply.​

Answer 1

• y =
  `(2)/(3)`x - 8 and y = -
  `(3)/(2)`x - 8
• y = x + 2 and y = -x + 3
• y = 3 and x = 4
• y =
  `(4)/(5)`x - 8 and y = -
  `(5)/(4)`x + 3

Explanation:

Two lines are perpendicular to each other if the product of their slopes is -1

In the case of lines y = 3 and x = 4 , their slopes are zero and infinite respectively but this two lines are by construction perpendicular to each other.

Answer 2

The correct options are: B, C, E and F

Explanation:

Consider the provided information.

Two lines are said to be perpendicular if the slopes are opposite reciprocals.

`m_1* m_2=-1`

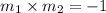
The slope intercept form is:
`y=mx+c`

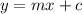
Where m is the slope of line.

Now consider the provided options:

Option A)
`y=(2)/(3)x+4\ and\ y= (2)/(3)x-8`

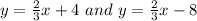
Both the equation have same slope i.e 2/3.

Thus, the pair of line is not perpendicular.

Option B)
`y=(2)/(3)x-8\ and\ y= -(3)/(2)x-8`

`(2)/(3)* -(3)/(2)=-1`

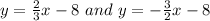
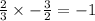
Hence, the pair of line is perpendicular.

Option C)
`y=x+2\ and\ y= -x+3`

`1* (1)/(-1)=-1`

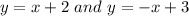
Hence, the pair of line is perpendicular.

Option D)
`y=3x+2\ and\ y=3x-2`

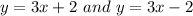
Both the equation have same slope i.e 3.

Thus, the pair of line is not perpendicular.

Option E)
`y=3\ and\ x=4`

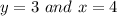
y=3 is a horizontal line parallel to x-axis and x=4 is a vertical line parallel to y axis. We know that x and y axis are perpendicular to each other and the provided lines follows the same property.

Thus, the pair of line is perpendicular.

Option F)
`y=(4)/(5)x-8\ and\ y= -(5)/(4)x+3`

`(4)/(5)* -(5)/(4)=-1`

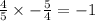
Thus, the pair of line is perpendicular.

Hence, the correct options are: B, C, E and F