Question

Which expression is equivalent to (x^27 y)^1/3

Answer 1

`\large\boxed{\left(x^(27)y\right)^(1)/(3)=x^9y^(1)/(3)=x^9\sqrt[3]{y}}`

Explanation:

`\left(x^(27)y\right)^(1)/(3)\qquad\text{use}\ (ab)^n=a^nb^n\ \text{and}\ (a^n)^m=a^(nm)\\\\\left(x^(27)\right)^(1)/(3)y^(1)/(3)=x^{(27)\left((1)/(3)\right)}y^(1)/(3)=x^9y^(1)/(3)\\\\\text{use}\ a^(1)/(n)=\sqrt[n]{a}\\\\=x^9\sqrt[3]{y}`

Answer 2

The equivalent form of the given expression is
`x^(9)*\sqrt[3]{y}`

Explanation:

Given : Expression
`(x^(27)y)^(1)/(3)`

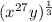
To find : The expression is equivalent to?

Solution :

Step 1 - Write the expression

`(x^(27)y)^(1)/(3)`

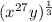
Step 2 - Separating the power using
`(xy)^a=x^a* y^a`

`=(x^(27))^{(1)/(3)}* y^{(1)/(3)}`

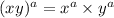
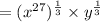
Step 3 - Solving the power,
`(x^a)^b=x^(a* b)`

`=x^{27*(1)/(3)}* y^{(1)/(3)}`

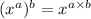
Step 4 - Simplifying

`=x^(9)*\sqrt[3]{y}`

So, The equivalent form of the given expression is
`x^(9)*\sqrt[3]{y}`