Question

Which of the following is not an identity?

Answer 1

Option A.

Explanation:

The first equation is

`2\sin^2x-\sin x=1`

Taking LHS,

`LHS=2\sin^2x-\sin x`

Substitute x=0 in the given equation.

`LHS=2\sin^2(0)-\sin (0)`

`LHS=0\\eq 1`

`LHS\\eq RHS`

The equation
`2\sin^2x-\sin x=1` is not an identity, therefore the correct option is A.

The second equation is

`\sec x\csc x(\tan x+\cot x)=\sec^2x+\csc^2x`

Taking LHS,

`LHS=\sec x\csc x(\tan x+\cot x)`

`LHS=\sec x\csc x\tan x+\sec x\csc x\cot x`

`LHS=(1)/(\cos x)\cdot (1)/(\sin x)\cdot (\sin x)/(\cos x)+(1)/(\cos x)\cdot (1)/(\sin x) \cdot (\cos x)/(\sin x)`

`LHS=(1)/(\cos^2 x)+(1)/(\sin^2 x)`

`LHS=\sec^2 x\csc^2 x`

`LHS=RHS`

The equation
`\sec x\csc x(\tan x+\cot x)=\sec^2x+\csc^2x` is an identity.

The third equation is

`2\cos^2x-1=1-2\sin^2x`

We know that

`\cos 2x=2\cos^2 x-1`

`\cos 2x=1-2\sin^2 x`

Equating these two equation we get

`2\cos^2x-1=1-2\sin^2x`

The equation
`2\cos^2x-1=1-2\sin^2x` is an identity.

The fourth equation is

`\sin^2x+\tan^2x+\cos^2x=\sec^2x`

Taking LHS,

`LHS=\sin^2x+\tan^2x+\cos^2x`

`LHS=(\sin^2x+\cos^2x)+\tan^2x`

`LHS=1+\tan^2x`
`[\because \sin^2x+\cos^2x=1]`

`LHS=\sec^2x`
`[\because 1+\tan^2x=\sec^2x]`

`LHS=RHS`

The equation
`\sin^2x+\tan^2x+\cos^2x=\sec^2x` is an identity.

Answer 2

The expression that is not an identity is:

Option: A
`2\sin^2 x-\sin x=1`

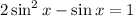
Explanation:

Option: A

`2\sin^2 x-\sin x=1`

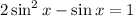
We may check this identity at a point.

when x=0 we have:

`2\sin^2 0-\sin 0=1\\\\0-0=1\\\\0=1`

which is not possible.

Hence, identity A is incorrect.

Option: B

`\sec x\csc x(\tan x+\cot x)=\sec^2x+\csc^2 x`

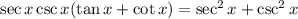
On taking the left hand side of the expression we have:

`\sec x\csc x(\tan x+\cot x)=(1)/(\cos x)\cdot (1)/(\sin x)((\sin x)/(\cos x)+(\cos x)/(\sin x))\\\\\\\sec x\csc x(\tan x+\cot x)=(1)/(\cos x\sin x)\cdot ((\sin^2 x+\cos ^2x)/(\sin x\cos x))\\\\\\\sec x\csc x(\tan x+\cot x)=(\sin^2 x+\cos^2 x)/(\sin^2 x\cos^2 x)\\\\\\\sec x\csc x(\tan x+\cot x)=(\sin^2 x)/(\sin^2 x\cos^2 x)+(\cos^2 x)/(\sin^2 x\cos^2 x)\\\\\\\sec x\csc x(\tan x+\cot x)=(1)/(\cos^2 x)+(1)/(\sin^2 x)`

`\sec x\csc x(\tan x+\cot x)=\sec^2 x+\csc^2 x`

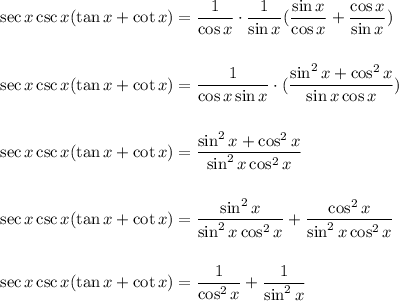
Hence, option: B is correct.

Option: C

We know that:

`\cos 2x=1-2\sin^2 x`

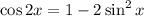
and
`\cos 2x=2\cos^2 x-1`

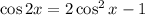
Hence, we get:

`1-2\sin^2 x=2\cos^2 x-1`

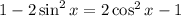
Hence, option: C is correct.

Option: D

`\sin^2 x+\tan^2 x+\cos^2 x=\sec^2 x`

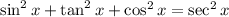
On taking left hand side we get:

`\sin^2 x+\tan^2 x+\cos^2 x=\sin^2 x+\cos^2 x+\tan^2 x\\\\\\\sin^2 x+\tan^2 x+\cos^2 x=1+\tan^2 x\\\\\\\sin^2 x+\tan^2 x+\cos^2 x=\sec^2 x`

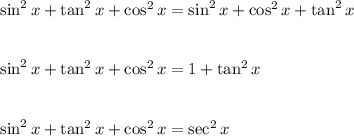
Hence, option: D is correct.